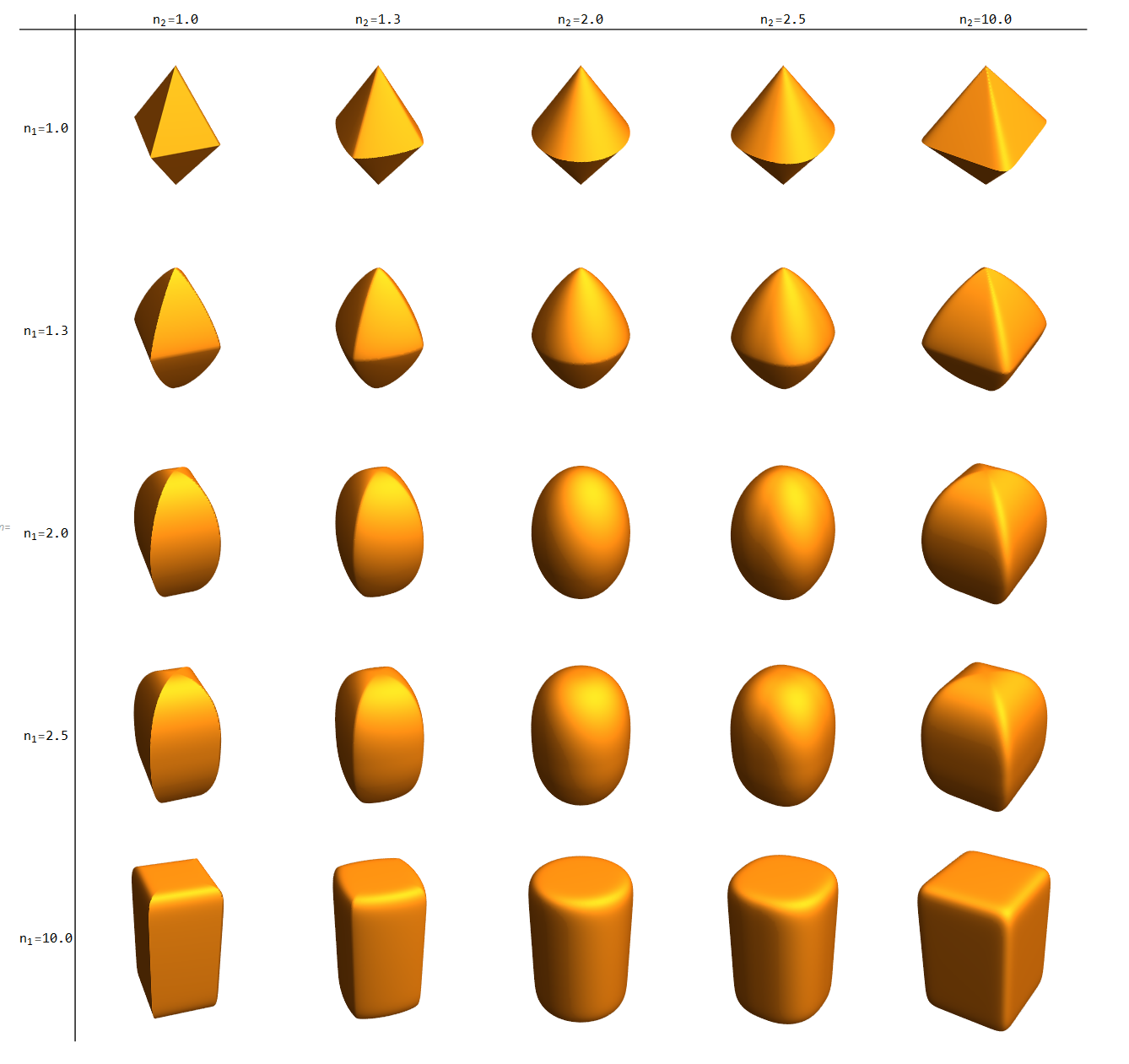生成土颗粒
昨天听 Jun Yang 的讲座,看到如下图所示的用于生成不同土颗粒形状的公式,看起来还挺有意思。
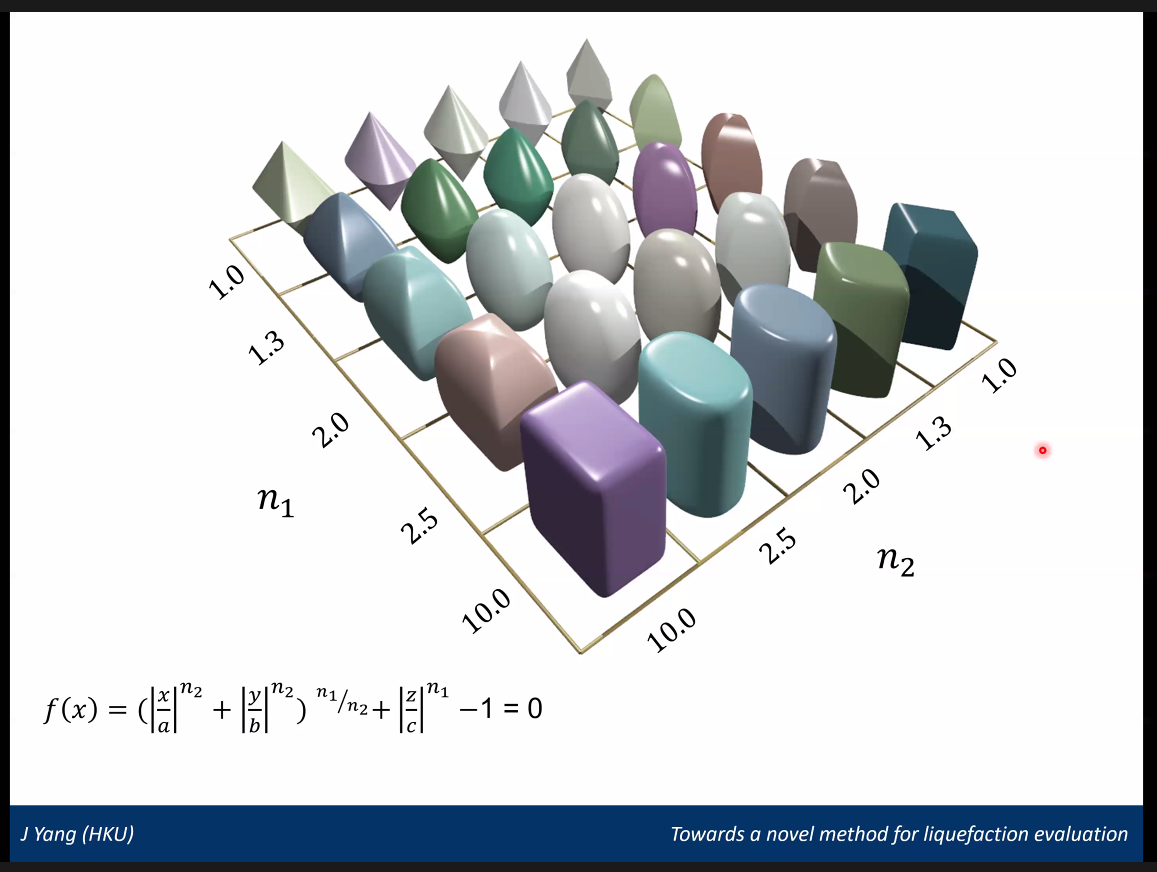

用于生成颗粒形状的公式为:
\[f(x,y,z)=\left( \left\vert\dfrac{x}{a} \right\vert^{n_2} + \left \vert\dfrac{y}{b} \right\vert^{n_2} \right)^{n_1/n_2} + \left\vert\dfrac{z}{c} \right\vert^{n_1} - 1 =0\]大概可以看出 $a$,$b$,$c$ 分别对应于 $x$,$y$ 和 $z$ 轴方向的「长度」,$n_1$ 和 $n_2$ 控制相关的弯曲情况。
简单例子
先看一个简单的例子。
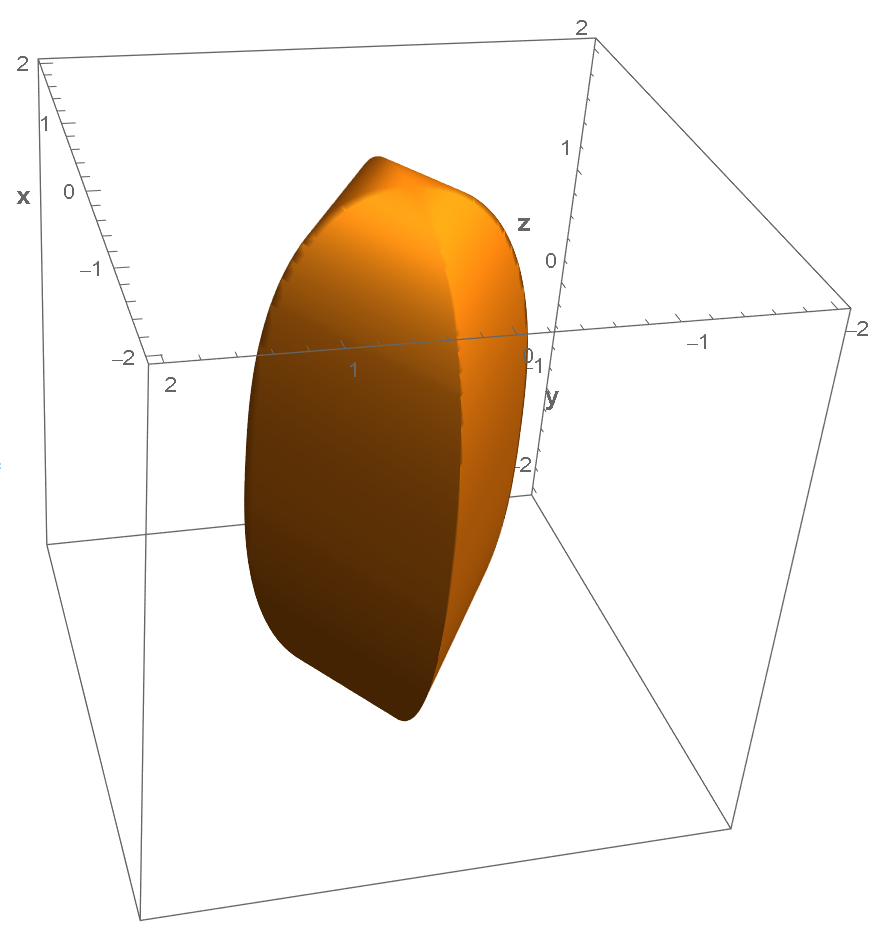
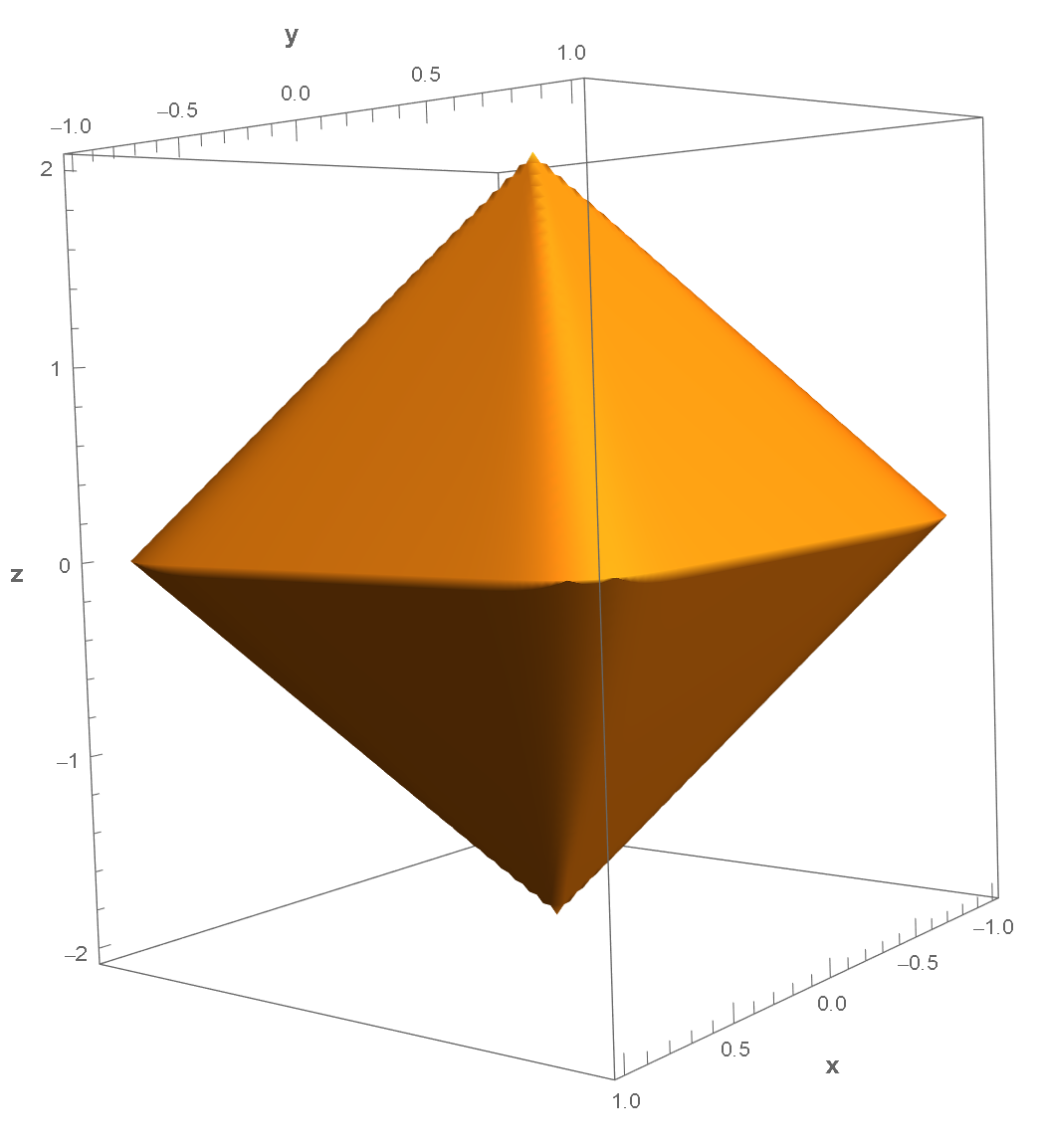
让 $n_1=2.5$,$n_2=1.0$,$a=1.5$,$b=1$,$c=2$:
Block[
{n1 = 2.5, n2 = 1.0, a = 1.5, b = 1, c = 2},
ContourPlot3D[(Abs[x/a]^n2 + Abs[y/b]^n2)^(n1/n2) + Abs[z/c]^n1 -
1 == 0, {x, -2, 2}, {y, -2, 2}, {z, -2, 2},
Mesh -> None,
AxesLabel -> (Style[#, Bold, 12] & /@ {"x", "y", "z"}),
PerformanceGoal -> "Quality",
Method -> {"BoundaryOffset" -> False}
]
]
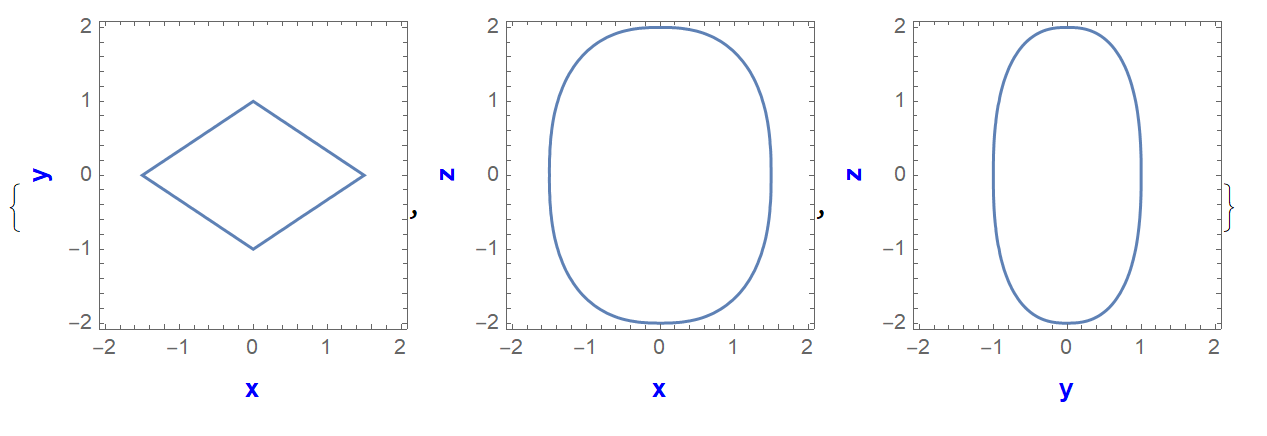
同样将其在 $x-y$,$x-z$,$y-z$ 平面的投影画出来:
Block[
{f, n1 = 2.5, n2 = 1.0, a = 1.5, b = 1, c = 2, xy, xz, yz},
f[x_, y_, z_] := (Abs[x/a]^n2 + Abs[y/b]^n2)^(n1/n2) + Abs[z/c]^n1 -
1;
xy =
ContourPlot[f[x, y, 0] == 0, {x, -2, 2}, {y, -2, 2},
Mesh -> None,
FrameLabel -> (Style[#, Bold, Blue, 12] & /@ {"x", "y"})
];
xz =
ContourPlot[f[x, 0, z] == 0, {x, -2, 2}, {z, -2, 2},
Mesh -> None,
FrameLabel -> (Style[#, Bold, Blue, 12] & /@ {"x", "z"})
];
yz = ContourPlot[f[0, y, z] == 0, {y, -2, 2}, {z, -2, 2},
Mesh -> None,
FrameLabel -> (Style[#, Bold, Blue, 12] & /@ {"y", "z"})
];
{xy, xz, yz}
]
可以清楚看出 $a$,$b$,$c$ 所对应的几何意义。另外,因为 $n_2=1$,所以 在固定 $z$ 的情况下,$x$ 和 $y$ 为线性关系,即 $n_2$ 控制了在固定 $z$ 下 $x$ 和 $y$ 之间的关系。$n_1$ 则控制了 $x$ 和 $y$ 整体与 $z$ 之间的关系。当然,为了更清楚看其几何意义,可以将 $x$ 或 $y$ 固定,$n_1$ 控制了上图中 $x-z$ 平面和 $y-z$ 平面投影的曲线的弯曲情况。
特殊情况
在下面的示例中,我们固定 $a=b=1$,$c=2$。我们查看不同 $n_1$ 和 $n_2$ 对颗粒形状的影响。
$n_1$ 和 $n_2$ 都比较小
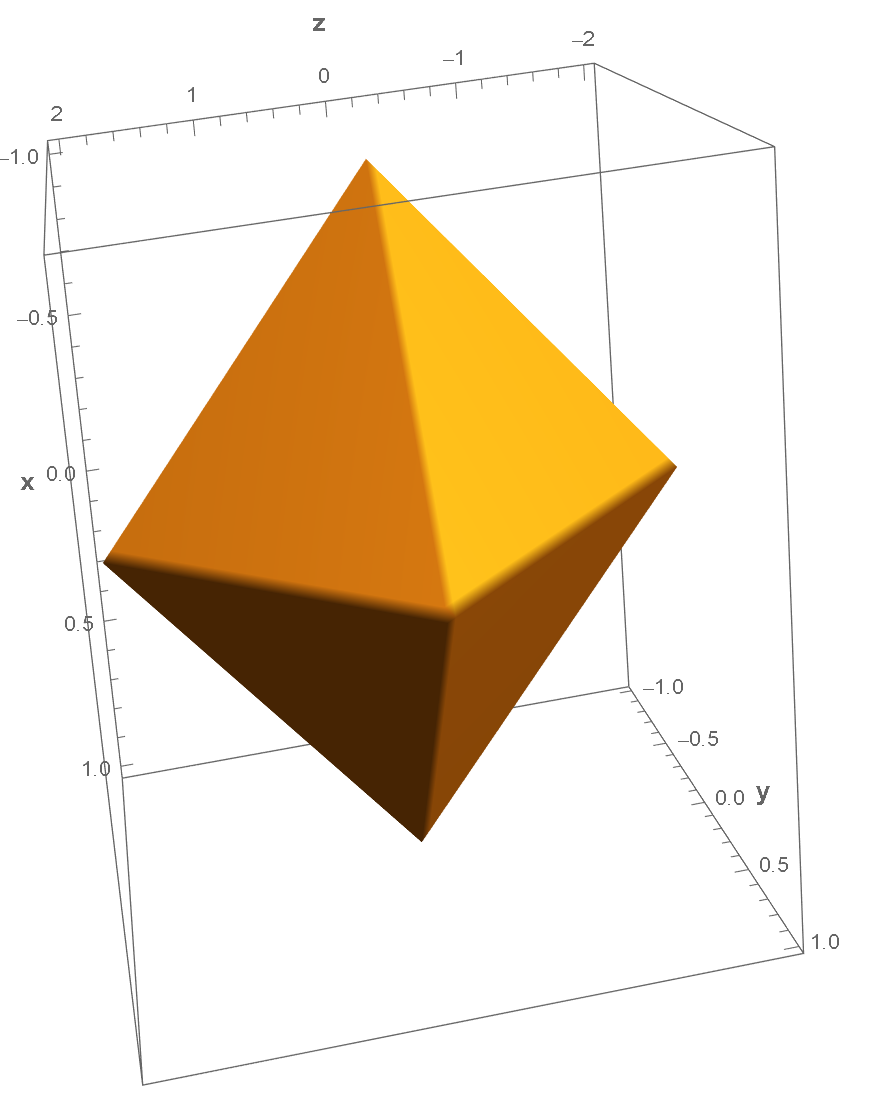
比如,如果 $n_1=n_2=1$,则上述的公式简化为:
\[f(x,y,z)= \left\vert\dfrac{x}{a} \right\vert+ \left\vert \dfrac{y}{b} \right\vert + \left\vert \dfrac{z}{c} \right\vert - 1 =0\]很显然,这描述的是在空间上有「线性」平面组成的颗粒形状。
Block[
{f, n1 = 1, n2 = 1.0, a = 1, b = 1, c = 2},
f[x_, y_, z_] := (Abs[x/a]^n2 + Abs[y/b]^n2)^(n1/n2) + Abs[z/c]^n1 -
1;
ContourPlot3D[f[x, y, z] == 0, {x, -1, 1}, {y, -1, 1}, {z, -2, 2},
Mesh -> None,
AxesLabel -> (Style[#, Bold, 12] & /@ {"x", "y", "z"}),
AspectRatio -> Full,
PerformanceGoal -> "Quality",
Method -> {"BoundaryOffset" -> False}
]
]
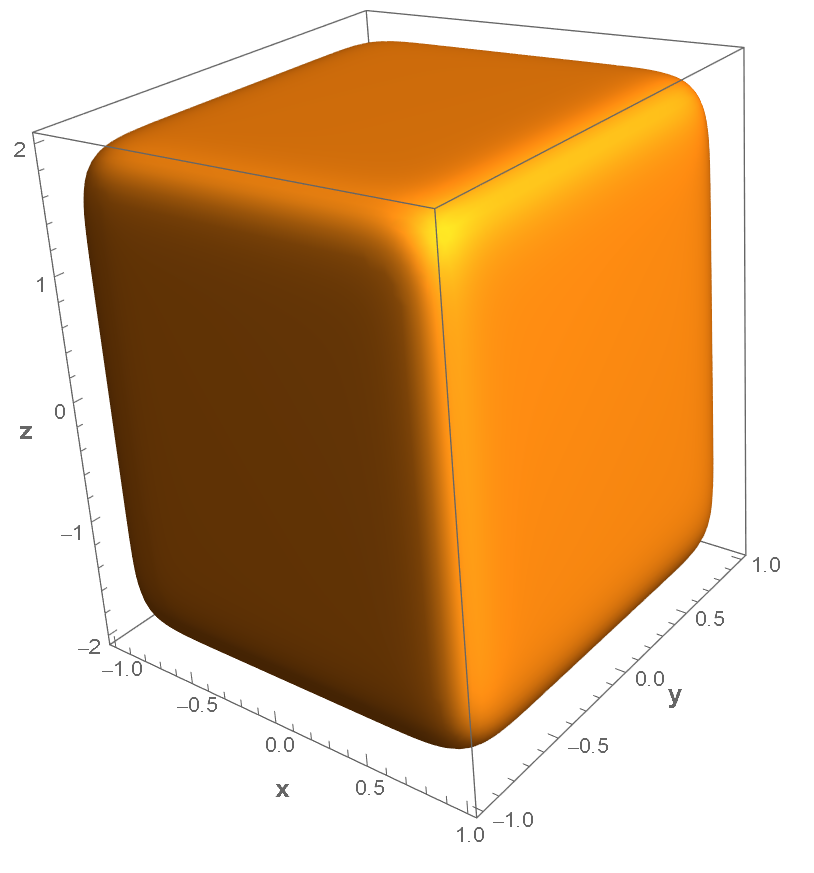
$n_1$ 和 $n_2$ 都比较大
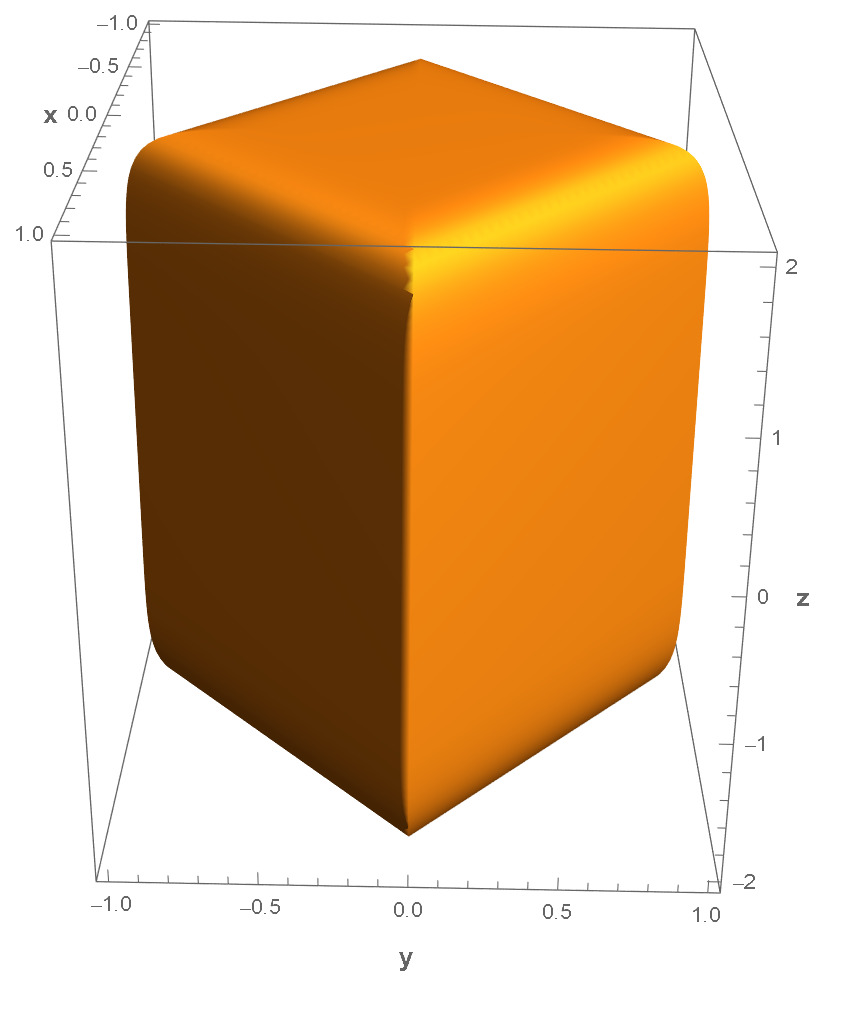
如果 $n_1$ 和 $n_2$ 都比较大,比如 $n_1=n_2=10$,则如果 $x <a$ (或者 $y<b$,$z<c$),则该项就会非常小,其他坐标就会趋于一个常数,因此整体就会趋于一个六面体。
Block[
{f, n1 = 10, n2 = 10, a = 1, b = 1, c = 2},
f[x_, y_, z_] := (Abs[x/a]^n2 + Abs[y/b]^n2)^(n1/n2) + Abs[z/c]^n1 -
1;
ContourPlot3D[f[x, y, z] == 0, {x, -1, 1}, {y, -1, 1}, {z, -2, 2},
Mesh -> None,
AxesLabel -> (Style[#, Bold, 12] & /@ {"x", "y", "z"}),
AspectRatio -> Full,
PerformanceGoal -> "Quality",
Method -> {"BoundaryOffset" -> False}
]
]
$n_1$ 比较小,$n_2$ 比较大
如果 $n_1$ 比较小,$n_2$ 比较大,比如 $n_1=1$,$n_2=10$,则如果固定 $z$,在 $x-y$ 平面的投影将是个矩形,而固定 $x$ (或 $y$),$y-z$ (或 $x-z$ )将趋于线性。
Block[
{f, n1 = 1, n2 = 10, a = 1, b = 1, c = 2},
f[x_, y_, z_] := (Abs[x/a]^n2 + Abs[y/b]^n2)^(n1/n2) + Abs[z/c]^n1 -
1;
ContourPlot3D[f[x, y, z] == 0, {x, -1, 1}, {y, -1, 1}, {z, -2, 2},
Mesh -> None,
AxesLabel -> (Style[#, Bold, 12] & /@ {"x", "y", "z"}),
AspectRatio -> Full,
PerformanceGoal -> "Quality",
Method -> {"BoundaryOffset" -> False}
]
]
$n_1$ 比较大,$n_2$ 比较小
如果 $n_1$ 比较大,$n_2$ 比较小,比如 $n_1=10$,$n_2=1$,则如果固定 $z$, $x-y$ 曲线趋于线性,而固定 $x$ (或 $y$),$y-z$ (或 $x-z$ )将趋于矩形。
Block[
{f, n1 = 10, n2 = 1, a = 1, b = 1, c = 2},
f[x_, y_, z_] := (Abs[x/a]^n2 + Abs[y/b]^n2)^(n1/n2) + Abs[z/c]^n1 -
1;
ContourPlot3D[f[x, y, z] == 0, {x, -1, 1}, {y, -1, 1}, {z, -2, 2},
Mesh -> None,
AxesLabel -> (Style[#, Bold, 12] & /@ {"x", "y", "z"}),
AspectRatio -> Full,
PerformanceGoal -> "Quality",
Method -> {"BoundaryOffset" -> False}
]
]
适中的 $n_1$ 和 $n_2$
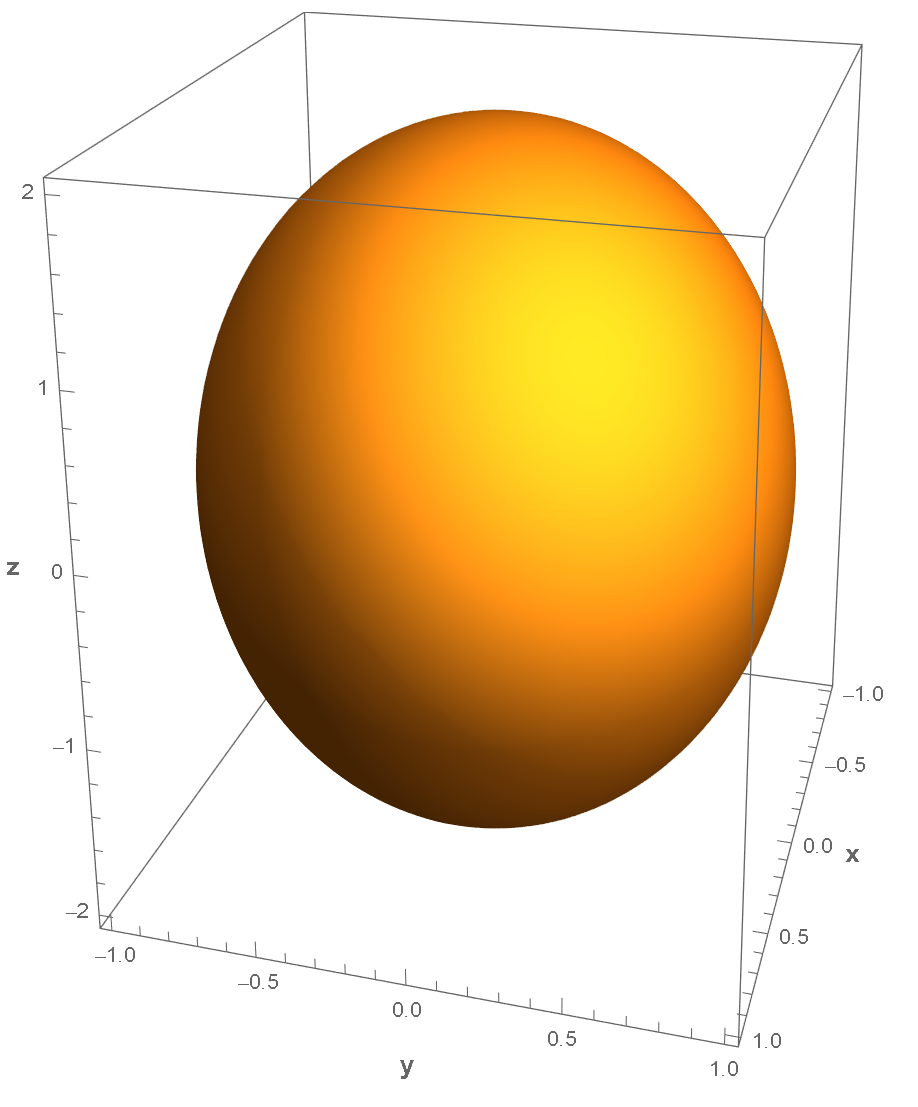
可以想象,适中的 $n_1$ 和 $n_2$ (比如 $n_1=n_2=2$)将会得到比较光滑的曲面。
Block[
{f, n1 = 2, n2 = 2, a = 1, b = 1, c = 2},
f[x_, y_, z_] := (Abs[x/a]^n2 + Abs[y/b]^n2)^(n1/n2) + Abs[z/c]^n1 -
1;
ContourPlot3D[f[x, y, z] == 0, {x, -1, 1}, {y, -1, 1}, {z, -2, 2},
Mesh -> None,
AxesLabel -> (Style[#, Bold, 12] & /@ {"x", "y", "z"}),
AspectRatio -> Full,
PerformanceGoal -> "Quality",
Method -> {"BoundaryOffset" -> False}
]
]
上面的代码画图的部分可以整到一个函数里面,我这里偷懒了。
不同情况
这里重现下 ppt 里面展示的不同 $n_1$ 和 $n_2$ 产生的颗粒形状。
Block[
{f, a = 1, b = 1, c = 1.5, plot, n1list, n2list},
f[x_, y_, z_, n1_, n2_] := (Abs[x/a]^n2 + Abs[y/b]^n2)^(n1/n2) +
Abs[z/c]^n1 - 1;
plot[n1_, n2_] :=
ContourPlot3D[
f[x, y, z, n1, n2] == 0, {x, -a, a}, {y, -b, b}, {z, -c, c},
Mesh -> None,
Axes -> False,
Boxed -> False,
AxesLabel -> (Style[#, Bold, 12] & /@ {"x", "y", "z"}),
BoxRatios -> Full,
PerformanceGoal -> "Quality",
Method -> {"BoundaryOffset" -> False},
PlotRangePadding -> None
];
n1list = {1.0, 1.3, 2.0, 2.5, 10.0};
n2list = {1.0, 1.3, 2.0, 2.5, 10.0};
TableForm[Table[plot[n1, n2], {n1, n1list}, {n2, n2list}],
TableHeadings -> {("\!\(\*SubscriptBox[\(n\), \(1\)]\)=" <>
ToString[NumberForm[#, {Infinity, 1}]]) & /@
n1list, ("\!\(\*SubscriptBox[\(n\), \(2\)]\)=" <>
ToString[NumberForm[#, {Infinity, 1}]]) & /@ n2list},
TableAlignments -> Center,
TableSpacing -> {0, 0}
]
]
生成不同形状的颗粒还只是第一步,生成互相不重叠的具有一定孔隙比的颗粒堆才是麻烦的开始。