全素数日期和分饼问题

逛微博看到的两个题目，随手写下。我好会浪费时间…

全素数日期

今天是 2019 年 5 月 23 日, 如果写成 20190523, 我们发现不断去掉这个数的头位数后, 剩下的数会都是素数¹, 即: 20190523, 0190523, 190523, 90523, 0523, 523, 23, 3 都是素数.

我们用 Mathematica 中的整数位数分解实现下:

1. 整数位数分解: IntegerDigits[20190523], 可得到 {2, 0, 1, 9, 0, 5, 2, 3};

2. 对上述得到的数位列表不断去掉第一个元素, 可以结合 Rest 和 NestWhileList : list = NestWhileList[Rest, {2, 0, 1, 9, 0, 5, 2, 3}, Length[#]>1&], 可得到: {{2, 0, 1, 9, 0, 5, 2, 3}, {0, 1, 9, 0, 5, 2, 3}, {1, 9, 0, 5, 2, 3}, {9, 0, 5, 2, 3}, {0, 5, 2, 3}, {5, 2, 3}, {2, 3}, {3}};

3. 把 2 中得到的列表每一次列表 sublist 的数位组装成整数: list2 = FromDigits/@ list;
4. 判断是否所有都是素数: And@@PrimeQ[list2].

综合起来就是:

allPrimeQ[n_] := 
 And @@ PrimeQ[
   FromDigits /@ 
    NestWhileList[Rest, IntegerDigits[n], Length[#] > 1 &]]

我们可以寻找下 2019 年还有什么日期也是这样的.

先把 2019 年所有日期写成上述数字的形式:

ToExpression@DateString[#, {"Year", "Month", "Day"}] & /@ 
 DateRange[{2019, 01, 01}, {2019, 12, 31}]

从中找出 allPrimeQ 为 true 的日期:

Select[ToExpression@DateString[#, {"Year", "Month", "Day"}] & /@ 
  DateRange[{2019, 01, 01}, {2019, 12, 31}], allPrimeQ]
  
  (*{20190523, 20190823}*)

即 2019 年除了 5 月 23 日, 还有 8 月 23 日也是素数.

Julia 代码:

using Primes
using Dates

function all_prime(n::Int64)
    digitlist = reverse(digits(n))
    prime_test = Bool[]
    for i in 1:length(digitlist)
        push!(prime_test, isprime(foldl((x,y)->x*10+y, digitlist[i:end])))
    end
    all(prime_test)
end

datelist = [parse(Int64, Dates.format(x,"yyyymmdd")) for x in Dates.Date(2019, 1, 1):Dates.Day(1):Dates.Date(2019, 12, 31)];

datelist[findall(all_prime, datelist)]

分饼问题

微博”密西西比量子猪”的问题:

有一个大饼，第一个客人得1%，第二个客人得剩下的2%，第三个客人得剩下的3%……. 问：第几个客人会得到最多的饼？

解答过程如下.

我们假定第 $n$ 个人还没分时, 剩下 $f_{n-1}$, 分完后剩余 $f_n = (1-\dfrac{n}{100})f_{n-1}$, 则第 $n$ 个客人分到 $a_n = \dfrac{n}{100} \cdot f_{n-1}$, 第 $n+1$ 个客人分到 $a_{n+1} = \dfrac{n+1}{100} \cdot f_{n} = \dfrac{n+1}{100} (1-\dfrac{n}{100})f_{n-1}$. 因此先后两个客人分到的饼比值为: $\dfrac{a_{n+1}}{a_n} = \dfrac{(n+1)(1-\frac{n}{100})}{n}$. 由 $\dfrac{a_{n+1}}{a_n} < 1$ 可得当 $ n \ge 10$ 时, $\dfrac{a_{n+1}}{a_n} < 1$, 当 $n< 10$ 时, $\dfrac{a_{n+1}}{a_n} > 1$. 即第 10 个客人会得到最多的饼. 尝试了寻找其通项, 发现不是一般地麻烦…

Mathematica 暴力求解…

Block[{f, a},
 f[0] = 1;
 f[n_] := f[n] = (1 - n/100) f[n - 1];
 a[n_] := f[n - 1] - f[n];
 Print[{a[10], a[10] // N}];
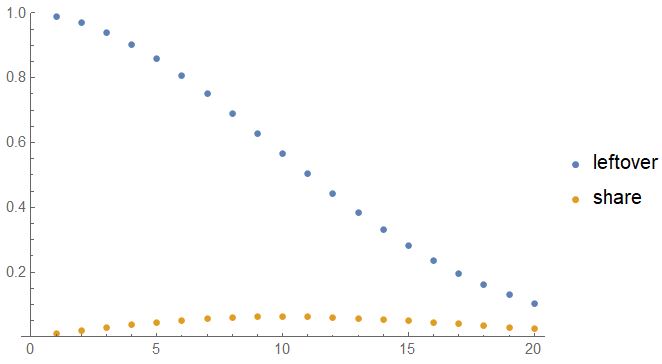
 ListPlot[{Table[f[n], {n, Range[20]}], Table[a[n], {n, Range[20]}]}, 
  PlotRange -> {0, 1}, PlotLegends -> {"Leftover", "share"}]
 ]
 
 (*{245373636545037/3906250000000000,0.0628157}*)

Julia 代码:

using Plots

function leftover(n::Int64)
    n == 0 && return 1
    return (1 - n/100)*leftover(n-1)
end

function share(n::Int64)
    leftover(n-1) - leftover(n)
end

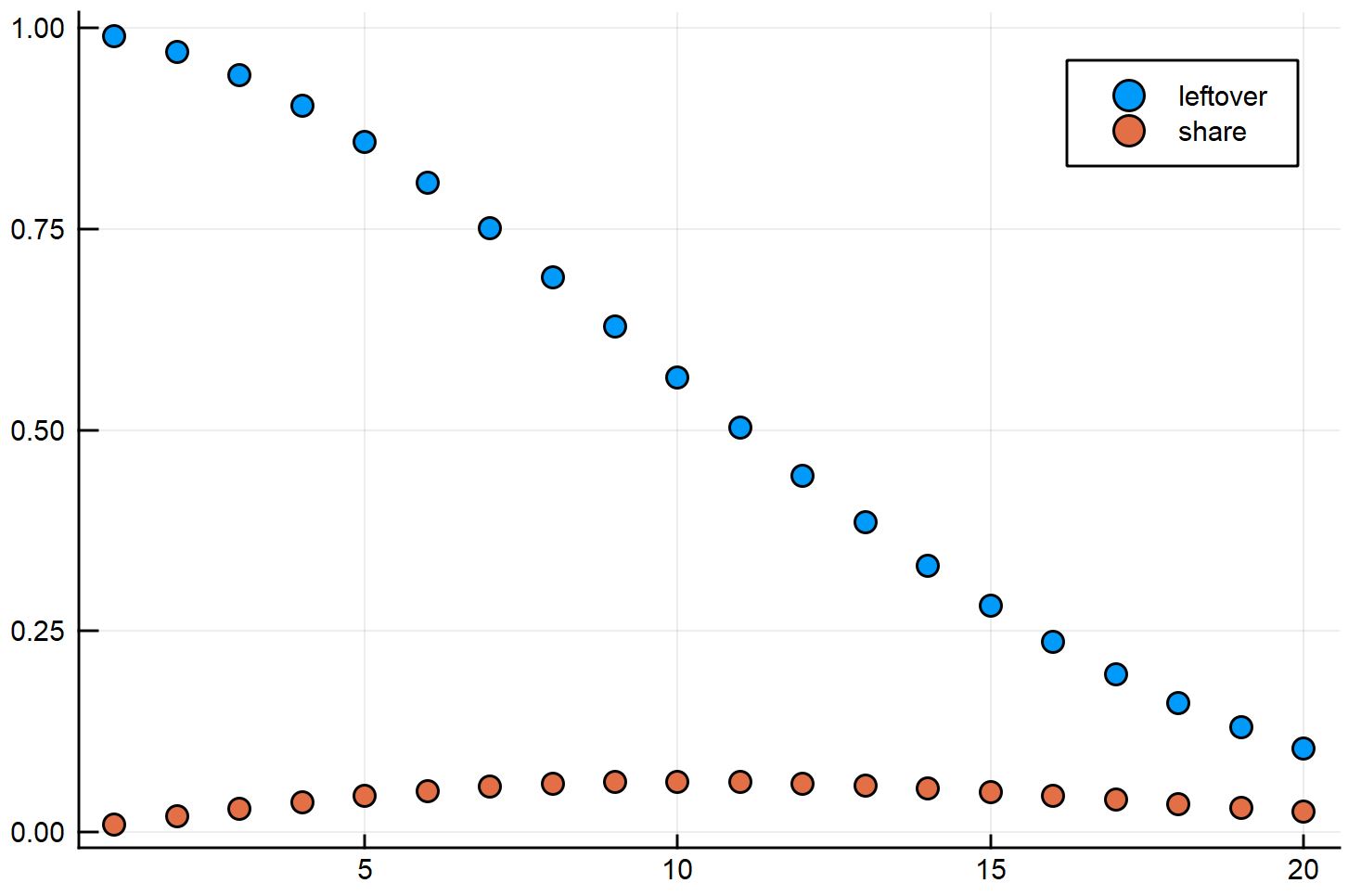
plot(1:20, [leftover(n) for n in 1:20], label="leftover", seriestype=:scatter)
plot!(1:20, [share(n) for n in 1:20], label="share", seriestype=:scatter)