有限元中的雅可比矩阵
有限元中单元的刚度矩阵通过简单推导后可表示为
\[\int_\Omega B^T DB \ \mathrm{d}\Omega\]在数值计算过程中, 为了求解上述积分, 需要做两方面的处理.
第一是用高斯积分近似求解, 如 $\displaystyle \int_{-1}^1 f(x) \ \mathrm{d}x \approx \sum_{i=1}^N w_i f(x_i) $, 其中, $x_i$ 为高斯点的位置, $w_i$ 为相应的权重1. 高斯积分同样可扩展到二维甚至三维的情况. 此处不再赘述. 值得说明的是, 这里为了求解以局部坐标 $(\xi, \eta)$ 表示的 $B$ 矩阵, 需要对雅可比矩阵 (事实上应该是下述雅可比矩阵的转置) 求逆.
第二是将 $(x,y)$ 的域转换到 $(\xi, \eta) \in [-1, 1] \times [-1,1]$ 上来, 主要是 $\displaystyle \iint_\Omega \mathrm{d}x \mathrm{d}y=\int_{-1}^1 \int_{-1}^1 \det{J} \ \mathrm{d}\xi \mathrm{d}\eta$. 证明如下.
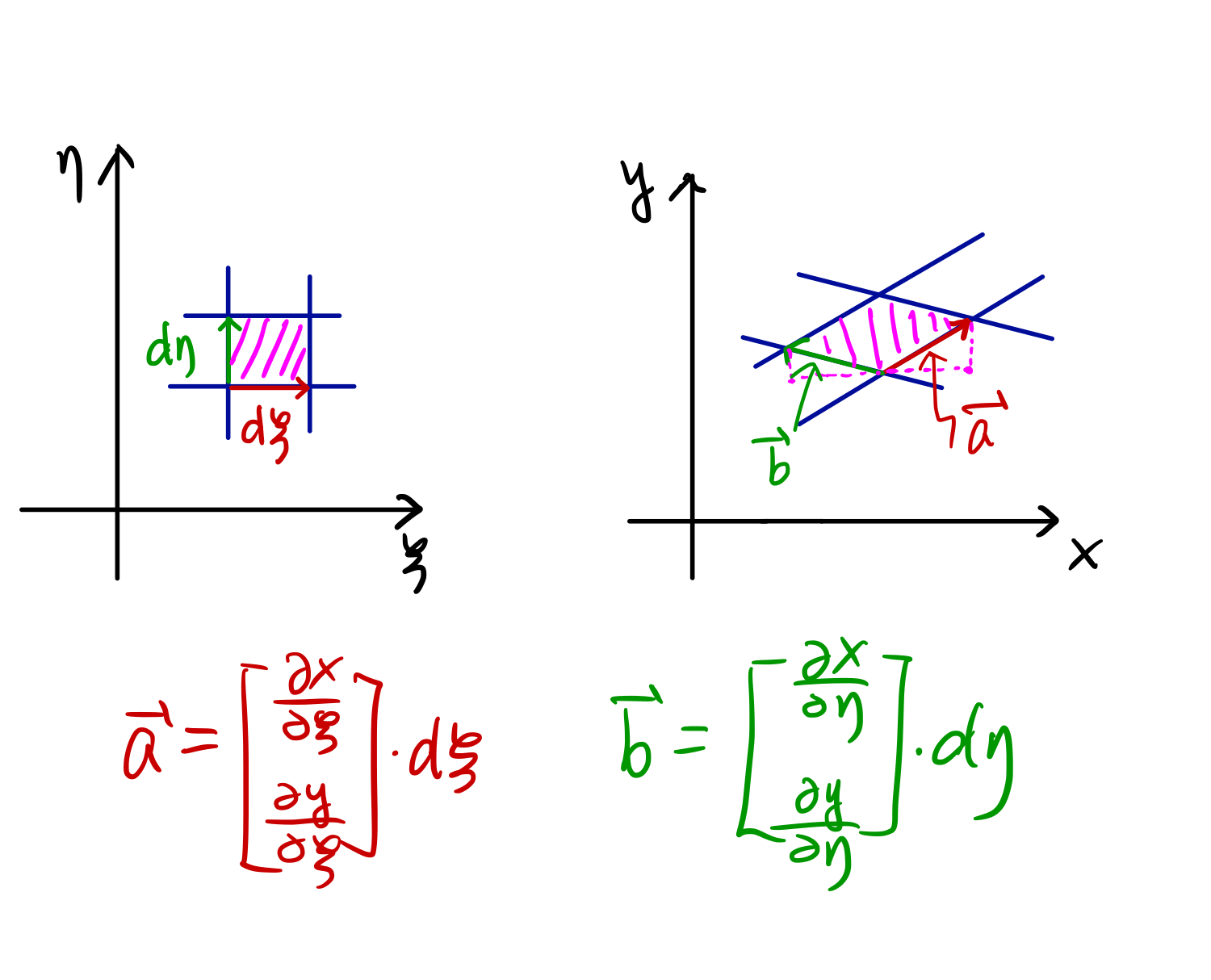如图所示, 将 $(\xi, \eta)$ 往 $(x,y)$ 上变换时, $(1,0)^T$ 将会变换到 $\left(\frac{\partial x}{\partial \xi}, \frac{\partial y}{\partial \xi}\right)^T$, $(0,1)$ 将会变换到 $\left(\frac{\partial x}{\partial \eta}, \frac{\partial y}{\partial \eta} \right)^T$, 根据线性变换 (局部线性) 的概念, 可得其变换矩阵为
此即为传说中的雅可比矩阵 (Jacobian matrix).
变换后的 “小格子” 的面积 (二维的向量叉乘2) 为
\[\mathrm{d}A = \vec{a}\times \vec{b} = \left(\dfrac{\partial x}{\partial \xi} \dfrac{\partial y}{\partial \eta}-\dfrac{\partial y}{\partial \xi}\dfrac{\partial x}{\partial \eta} \right) \mathrm{d}\xi \mathrm{d}\eta = \det{J} \ \mathrm{d}\xi \mathrm{d}\eta\]由此可得 $\displaystyle \iint_\Omega \mathrm{d}x \mathrm{d}y=\int_{-1}^1 \int_{-1}^1 \det{J} \ \mathrm{d}\xi \mathrm{d}\eta$.
雅可比矩阵描述坐标变换前后面积（体积）的变化倍数, 因此, 一个单元越”畸形”, 其雅可比矩阵的行列式会越小, 当单元变形到翻转过来时, 雅可比矩阵的行列式为负值. 这些情况将导致雅可比矩阵的求逆变得更为困难, 计算也就更难收敛, 甚至会发生崩溃.
Ref: