此文为旧博客搬运。 ——2020.05.17

前不久同学询问关于前期勘察的一个问题：

比如在某一区域内，初期勘探了非均匀分布的 $n$ 个点 $pts$，勘探点上的 R 值为 $vals$，现要估算下区域内 R 的总量。

我想同学问我这个问题估计是想了解下用无网格法做做如何，我的第一反应是这个，不过跟无网格关系不大，无非是进行空间高阶近似插值而已。进一步想了下，更加没必要了，只要简单估算的话，我们只要用每个点所代表的面积（权重）乘以相应点上的值（当然我们假定该区域内 R 值为常数）就可以了。所以，关键是确定每个点所代表的区域面积。很自然的，就想到了 Voronoi Tessellation 了。这里用 Mathematica 简单实现了下。

首先我们假定该区域为 $5 \times 5$，勘察的点为 $pts$，相应的值为 $vals$， 我们用 RandomReal 随机生成（自然，实际数据可以通过 Import 导入）：

pts = RandomReal[5, {20, 2}];
vals = RandomReal[{5, 10}, 20];

为了后续方便，我们把点和其上的值关联起来:

assoc = Association[MapThread[Rule, {pts, vals}]];

在 Mathematica v10 以后，Voronoi Tessellation 可通过函数 VoronoiMesh 实现：

vor = VoronoiMesh[pts, {{0., 5.}, {0., 5.}}];

同时把 Voronoi mesh 和点画出来，并标出每个 cell 的编码（index）:

Show[HighlightMesh[
  vor, {Style[2, White], Style[1, Red], Labeled[2, "Index"]}], 
 Graphics[{PointSize[Medium], Blue, Point[pts]}]]

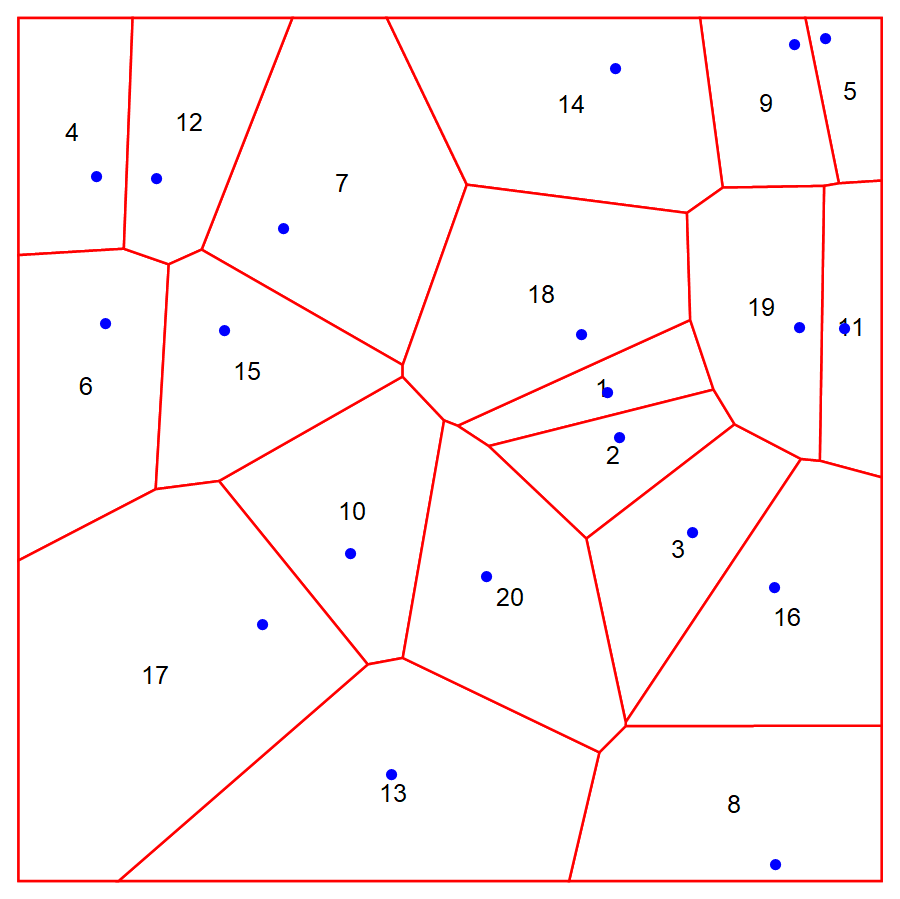
值得注意的是，这里 cell 的 index 跟点的顺序并没有对应。对于某个基于网格的区域 mr，可通过 RegionMeshMeshMemberCellIndex[mr, pt] 获取包含点 pt 的 cell index。

cind = Region`Mesh`MeshMemberCellIndex[vor];

每个 cell 的面积为：

areas = PropertyValue[{vor, 2}, MeshCellMeasure];

因此总的 R 值可以如下计算：

Part[areas, Last[cind[#]]]*assoc[#] & /@ pts // Total

合起来总的代码为：

ClearAll[pts, vals, assoc, vor, cind, areas];
SeedRandom[0];
pts = RandomReal[5, {20, 2}];
vals = RandomReal[{5, 10}, 20];
assoc = Association[MapThread[Rule, {pts, vals}]];
vor = VoronoiMesh[pts, {{0., 5.}, {0., 5.}}];
cind = Region`Mesh`MeshMemberCellIndex[vor];
areas = PropertyValue[{vor, 2}, MeshCellMeasure];
Part[areas, Last[cind[#]]]*assoc[#] & /@ pts // Total
Show[HighlightMesh[
  vor, {Style[2, White], Style[1, Red], Labeled[2, "Index"]}], 
 Graphics[{PointSize[Medium], Blue, Point[pts]}]]

参考