此文档为旧博客搬运。——2020.05.11

欧美影视剧里面酒吧总有话题，故事可以娓娓道来。如果有机会去酒吧，下面的故事也许可以讲讲。

在国内很少喝到黑啤，少数几次喝到的场合，好像大家因为其“异域”情调，有点把它当作高档酒了1，然而我却是怎么也想不起来那是什么味道了。世界上最出名的黑啤（dry stout）可能就是爱尔兰健力士公司酿造的健力士生世涛黑啤了（Guinness Drought Stout）。关于健力士黑啤，却有一个争议话题。

我们知道可乐里面气泡会不断上升，游泳时在水里吐气气泡也“汩汩”往上冒，那是因为浮力使得气泡往上升。而当酒吧里的人盯着健力士黑啤的杯子看时，情况可能就完全不一样了：他会发现气泡也会往下运动！这究竟是光学错觉还是真实的物理现象？或者是人们喝多了产生的错觉？健力士黑啤里的气泡到底是上升还是下沉？这个困扰人们两百多年的“世纪”难题成了酒吧里永恒的争议话题——也许还引发过不少争斗呢！想象一群壮汉因为这个话题而干起仗来，倒也颇有趣味。

世纪难题终于有了答案

这个传说中的世纪难题好像一直没人认真去解决，直到1999年澳大利亚新南威尔士大学（University of New South Wales）的 Clive Fletcher 教授通过计算流体动力学软件FLUENT 模拟了啤酒中气泡的运动情况。这一数值模拟并没有那么简单，需要考虑各种影响因素，如粘滞系数、密度、温度、几何形状等，“相较而言，模拟空调的气流或者供暖系统有毒气体的排放都变得极为简单”2。不管怎样，Fletcher教授的研究小组成功进行了啤酒中气泡的模拟，并研究了气泡尺寸对气泡运动模式的影响3 ，结果发现其原理出奇地“简单”。

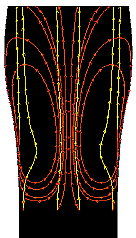图1. 气泡路径图显示大气泡（直径 $1\ \mathrm{mm}$）都往上升（黄色路线），而小气泡（直径 $60 \ \mu \mathrm{m}$）在杯子的边缘向下运动

图1 给出的是不同尺寸的气泡的运动路线图。其中红线表示的是小气泡的运动路径，其可以分解为如下几个过程：

  1. 当气泡从杯子底部开始升起时，因为杯子边缘对气泡的阻力（drag force）更大，因此杯子中间的气泡就比边缘气泡上升得快。气泡上升的同时“拖拽”着液体（即啤酒）跟着上升。
  2. 当液体到达表面后，就会往两边展开，推动边缘的液体往下运动。
  3. 往下运动的液体也会拖着边缘的气泡向下运动，当边缘气泡由此产生的向下运动速度超过其因浮力而上升的运动速度时，总的看来，边缘的气泡就会往下运动。
  4. 边缘气泡向下运动到达杯底后就会往杯子中间流动，从而形成一个闭环。

如果气泡比较大（如直径为 $1 \ \mathrm{mm}$），则边缘上的气泡受到的浮力较大，超过了边缘液体向下运动的拖拽作用，总体上就表现为往上运动，即不管是在杯子中间还是边缘，大气泡都会往上运动（图1中黄线）。

这个“世纪”难题终于有了答案：气泡既有上升，也有下沉！

怀疑与验证

然而学术界有这样一种现象：A numerical simulation is something nobody believes, except the person who made it. An experiment is something everybody believes, except the person who made it4 （除了做数值模拟的人自己别人都不相信他的结果，除了做实验的人自己别人都相信他的结果）。 Fletcher 教授的数值模拟结果出来后，有些人并不相信其结果，甚至怀疑他是不是真的喝多了。这“有些人”就包括斯坦福大学的 Dick Zare 教授。

Dick Zare 教授的小组在1998年5之后曾在酒吧做过一些初期实验，但并没有明确的结论。事实上Fletcher 教授刚开始也是和学生投入很大的精力呆在酒吧里观察，在喝了大量的健力士仍然一无所获后才转移到数值模拟上来。在2000年时 Zare 教授的小组使用常规的摄像机进行了拍摄，但仍然没有结论——那些气泡太小了，也动得太快了。在获悉Fletcher 教授的数值模拟后，他们才开始搬出“重武器”来认真验证下其结论。他们借来了每秒4500帧的高速摄像机，并用放大镜头放大气泡。

这一次，他们终于捕捉到了气泡的运动情况，并留下了影像“证据”—— Zare 教授的实验结果与 Fletcher 教授的数值模拟吻合得很好，即数值模拟和实验都验证了健力士黑啤边边缘气泡确实会下沉。当然，Zare 教授组也给出了相同的解释，如图2所示，其中第5步表示最终气泡都达到啤酒表面，形成所谓的啤酒“盖”（head）。

健力士的气泡下沉现象更容易被人观察到，得益于它的两个特点：一是健力士的气泡里面大部分是氮气，其形成的气泡更小6，因此更容易被液体“拽走”7；二是深色啤酒和浅色气泡反差大。那么对于其它“更不容易观察”的液体，是否有相同的现象呢？Fletcher教授给出的机理是否通用呢？实验结果给出了肯定的答案： Zare 教授小组分别对伯丁罕啤酒（Boddingtons）8 以及普通的水9（人为产生气泡）进行了观察，都发现了类似的气泡下沉的现象。——当然，是在没有喝酒的情况下！——不过也没酒可喝，实验用的啤酒都倒掉了。
第1步 第2步 第3步
第4步 第5步 循环图

图2. 气泡循环示意图

杯子形状的影响

Zare 教授的项目页面上有关于杯子形状的影响的问答是这样的：

Is the shape of the glass important?

The shape of the glass is not that important. We obtained similar results in curved and straight glasses. The pattern of flow will be different in the different shaped glasses, but not to the extent that would remove the effect.

不知这里所说的杯子的形状“会改变运动模式但不改变效应”具体是什么意思，因为形状不同气泡可能向上或向下，但是杯子、液体以及气泡之间的相互作用的模式是不变的？不管怎样，也确实有人继续研究了杯子形状对气泡运动的影响。2012年来自爱尔兰 Limerick 大学的 Benilov 教授采用了强大的多物理场耦合软件 COMSOL Multiphysics 进行了模拟，将健力士啤酒看成两相物质（气体和液体），并考虑气体—液体—固体之间的相互作用，研究了不同杯子形状时气泡的运动情况，模拟结果如图3所示（根据轴对称，只模拟了一个径向剖面）。

图3 “上宽下窄”（左图）和“上窄下宽”玻璃杯中气泡流动图

从图中可以看出，当杯子（爱尔兰常用的pint）为普通的上宽下窄时，杯边缘的液体会往下运动；而当杯子为上窄下宽时（anti-pint），杯边缘的液体反而向上运动。其解释也依赖于流体在杯子内部形成“环流”（circulation），不同的是对上升过程中气泡的不均匀现象给了另一种解释。

图4 “上宽下窄” （a） 和“上窄下宽”（b）玻璃杯中气泡的演化情况

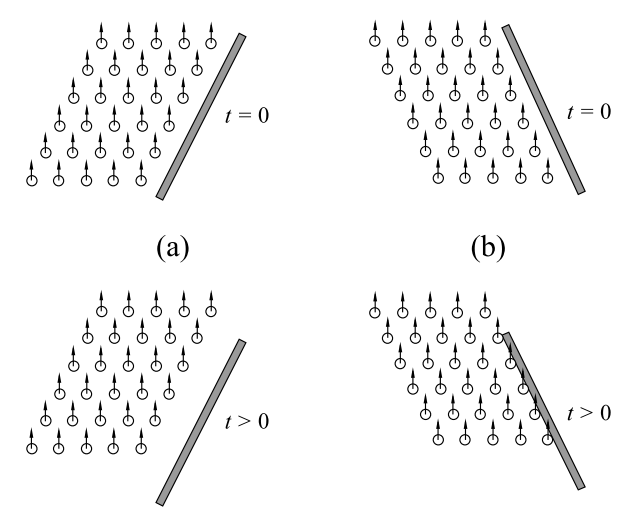
如图4所示，玻璃杯为“上宽下窄”时，当气泡上升后，边缘的气泡会扩散到往外更大的区域，从而使得靠近边缘区域的气泡密度降低，相较而言，杯子中间区域的气泡密度更大，其对液体的“拖拽”程度会更大，从而使得上部液体流向边缘，而边缘的液体带动气泡向下流动；当玻璃杯为“上窄下宽”时，气泡的上升使得玻璃边缘的气泡密度大于杯子中间区域的，相应的，边缘气泡对液体的“拖拽”作用更明显，即边边液体流动更快，从而流向中间区域，形成与前面相反的液体和气泡“环流”。——这其实也是悬浮系统沉淀中的Boycott效应10。

当然，为了不给人们对“数值模拟”留下“口实”，Benilov 他们还进行了实验验证，也留下了影像记录11。

结语

关于健力士泡沫运动的“争论”也许可以暂时停歇了，科学家已经从数值模拟和实际实验观察的角度12分别验证了健力士啤酒的泡沫确实会在杯边缘往下运动，但也不是只会向下运动。气泡运动的背后机理主要依赖于气泡——液体——杯子（固体）的相互作用：杯子与液体和气泡的相互接触或者杯子不同的形状引起了气泡的速度差异，差异运动的气泡拖拽液体形成杯内环流，环流继而“拖拽”气泡运动，而气泡同时受到液体的上浮力，拖拽力和上浮力之间的较量决定了气泡会往哪个方向运动。

科技论文或者新闻在文章的结尾大部分都要说明一下研究的潜在应用，生怕民众看了文章或者新闻以后觉得科学家在乱花纳税人的钱。关于研究健力士啤酒泡沫的意义，除了探索在不同边界条件下的流体力学外，Benilov 的文章结尾还提出了一个很有趣的问题：当前的啤酒杯子是否已经是最优的？是否可以通过改变杯子的形状来缩短啤酒气泡“安定”下来的时间？这是一个非常现实的问题，因为啤酒的“安定”时间影响了倒啤酒以及顾客喝上啤酒的时间。值得一提的是，跟啤酒气泡非常相似的一个问题——茶叶悖论13——被爱因斯坦用于解释流水侵蚀造就的河道弯曲问题；或许还有人们苦苦求索的未知领域，等着健力士啤酒气泡中的力学一展身手。

还有，如果你对前面提到的“太小”“太快”念念不忘的话，这是 Zare 教授的观察结果：从录像估算，健力士黑啤的气泡直径大概在$40 \sim 120 \mu \mathrm{m}$ 之间，跟头发的直径差不多；运动速度$2.11 ~ \mathrm{cm/s}$，即每秒大概动了$190$ 个“泡位”。

2017年7月16日 写于 香港

2017年7月21日 修改

参考资料

  1. 现在大家也没那么“崇洋媚外”，更多是一种“物以稀为贵”的想法吧。 ↩

  2. Kirk Kirksey, Aged-Old Beer Mystery Solved from Computer Factoids: Tales from the High-tech Underbelly. ↩

  3. Clive Fletcher研究的原网页已经打不开，Plus Math 的报道提到研究了杯子形状和气泡尺寸的影响，但是报道里只给出了气泡尺寸的结果，因此本文也只提气泡尺寸结果。 ↩

  4. 这句话应该是改编自爱因斯坦的话：A theory is something nobody believes, except the person who made it. An experiment is something everybody believes, except the person who made it. 从这句话也可以看出做数值的想发文章要比实验要难得多，前者除了要让自己相信，还要说服别人相信，而后者只要自己相信就可以了，而“要让自己相信”在巨大的 publish or perish 压力之前是很容易的。 ↩

  5. Zare 教授至少在1991年就已经与人合作写过 Through a Beer Glass Darkly，描述了啤酒气泡上升过程的模型——这帮“呆子”可能喝酒时实在无聊，只能盯着啤酒看了。 ↩

  6. 为什么氮气形成的气泡更小？ ↩

  7. 粘滞流体中的小球受到的阻力（或者“拖拽力”）与小球的尺寸（如半径）的一次方成正比，浮力与小球尺寸的三次方成正比，所以随着尺寸逐渐变大，先是“拖拽力”占优，大到一定程度时，则是浮力占优了。 ↩

  8. 一种英格兰啤酒，其罐装与健力士一样，都在罐里装有一种叫widget 的小塑料球，以释放大量细小气泡，让啤酒的口感更加绵柔。 ↩

  9. 值得说明的是，实验中健力士的粘滞系数和水很接近，所以对气泡运动的影响会差不多。 ↩

  10. 当试管倾斜时试管中红细胞的沉降速率大幅提高的现象，参见 Sedimentation of Blood Corpuscles http://www.nature.com/nature/journal/v104/n2621/abs/104532b0.html 和油管视频 https://www.youtube.com/watch?v=CFtteE5TuhI ↩

  11. 当然不是说留下影像记录别人就无话可说，比如数值模拟和实验得到的气泡“安定”（从倒入啤酒开始到冒泡结束）的时间并不一致（$43~ \mathrm{seconds} ~ \mathrm{vs} \ 120\ \mathrm{seconds}$），数值模拟假定气泡的特征尺寸为 $122 ~ \mu \mathrm{m}$，为球形，而实际气泡的尺寸有一定的分布（参见 Robinson, M., Fowler, A.C., Alexander, A.J. and O’Brien, S.B.G., 2008. Waves in Guinness. Physics of Fluids, 20(6), p.067101.）。数值模拟和实际实验总有一定的偏差，关键是能刻画其主要的物理现象甚至揭示其机理，比如气泡的流动模式。 ↩

  12. 还有比如从理论“解析”的角度研究健力士啤酒里面的波，以解释气泡的运动情况，见 Robinson, M., Fowler, A.C., Alexander, A.J. and O’Brien, S.B.G., 2008. Waves in Guinness. Physics of Fluids, 20(6), p.067101. ↩

  13. https://en.wikipedia.org/wiki/Tea_leaf_paradox ↩