“豹纹”是如何形成的

动物图案

阿兰·图灵 (Alan Turing) 被认为是上世纪最聪明的数学家之一。他在二战期间帮助破译了德国Enigma密码，并为电子计算机打下基础。他唯一一次进入数学生物领域就发表了一篇见地深刻的论文，在发表50年后仍然被大量引用。

网纹长颈鹿	罗斯柴尔德长颈鹿

模拟胚胎

图灵的文章描述了动物如何可能通过“反应-扩散方程”(reaction-diffusion equations)在胚胎发育期间产生图案模式。动物从开始的单个细胞不断分裂发育成最终完整的个体。在初始阶段，细胞小球是均一的(homogeneous)，但其后来却产生了如斑马、猎豹、长颈鹿、蝴蝶或者神仙鱼般多样的图案。空间上均一的系统，如均一的细胞小球，如何产生空间上不均一但是稳定的图案，如斑马的条纹？ 图灵对此产生了兴趣。他设法提出了 一系列的微分方程，解得该微分方程组，则可以巧妙地揭示动物身上多种多样的图案是如何产生的。

想象一个含有两种化学物质的胚胎。我们将会看到，该两种物质相互作用而形成图案，也因此被称为“成形素”(morphogens, 希腊语中 morpho 指形状， gen 指产生)。为了便于讨论，我们可以把胚胎想象成一维的线，并且研究线上每一点的两种成形素的浓度。成形素可以从高浓度的点向左右扩散到低浓度的点，也可以在胚胎细胞中重新生成。其中一种成形素称为“抑制物” (Inhibitor) ，可以抑制其自身以及另一种成形素的生成。另一种成形素叫“激活物” (Activator)，可以促进两种成形素的生成。

在胚胎任意点位置($x$) 以及任何时刻($t$)， 抑制物和激活物的浓度可分别用 $A(x,t)$ 和 $I(x,t)$ 表示。这些浓度会因为新生成（反应(reaction)）或者扩散(diffusion)而随时间变化。此系统也因此被称作反应-扩散方程 (reaction-diffusion equation)。

微分是获取曲线梯度——一个变量如何随另外一个变量的变化而变化——的方法。如果一个函数有两个变量（如此例），则求相对于其中一个变量的梯度称作偏微分。

激活物的浓度随时间的变化可写作以下偏微分方程

\[\frac{\delta A}{\delta t} = f(A,I)+\frac{\delta^2 A}{\delta x^2}\]

方程右侧第一项描述的是激活物是如何生成的，其为激活物和抑制物浓度的函数，因为二者都会影响反应的速率。方程右侧第二项是关于 $x$ 的二次偏导，描述了激活物梯度变化的快慢，即扩散的速率。 抑制物随时间的变化情况可写为

\[\frac{\delta I}{\delta t} = g(A,I)+d\frac{\delta^2 I}{\delta x^2}\]

方程右侧额外的项 $d$ 称作扩散系数，表征抑制物与激活物扩散速率的比值。图灵发现产生图案的关键因素是抑制物扩散比激活物要快。

微小扰动

刚开始时 ($t=0$)，这两种成形素处在平衡状态——他们的浓度不随时间而改变。激活物和抑制物的量都刚刚好，使得反应生成和扩散的速率刚好抵消。但这种状态是“不稳定平衡”，只要有个初始的推动——或者数学意义上的扰动——该系统就会偏离此平衡状态。这就像用笔尖竖立的铅笔，也许它是完全平衡的，但是只要简单的推动，铅笔就会倒掉，并且永远不会再回到平衡点。

不管何种原因，激活物的浓度在某一点微微增加。这样局部的激活物浓度就比抑制物的高，也就会生成更多的激活物，然后就像滚雪球一样继续增加。局部同时也生成了抑制物，但因其扩散比较快，抑制物迅速向扰动周边扩散，使得周边的激活物浓度降低。最终的结果是一片高浓度激活物的区域被高浓度的抑制物包围。整个过程可以从下图中看出。随着动画时间的改变，激活物的浓度沿着胚胎 ($x$轴) 逐渐形成一个个尖峰。

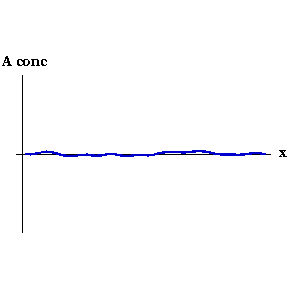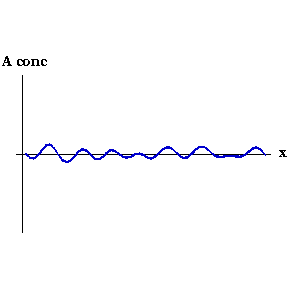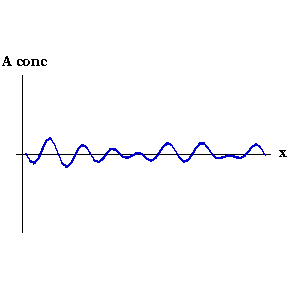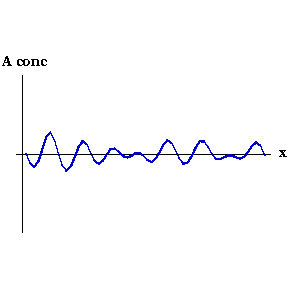激活物浓度 $A(x,t)$ 随时间变化

反应-扩散方程也可以在二维上展开。这样上述情况就变成了高浓度的激活物岛屿被抑制物护城河所围绕。该“护城河”再往外，抑制物的浓度又开始降低，别的扰动因此又可以在此形成高浓度激活物的区域。于是均匀对称的浓度分布就变成大致均匀分隔开的高浓度激活物区域。

图案呈现

激活物和抑制物本身并不是色素，只是相互作用形成底部“蓝图”的成形素。如果激活物也促进了动物皮肤里色素的生成，则图案就可以呈现出来了。假定皮肤细胞生成黄色色素，如果探测到了高浓度的激活物，则指导生成黑色色素。这样就可以产生类似于猎豹那样的图案了。

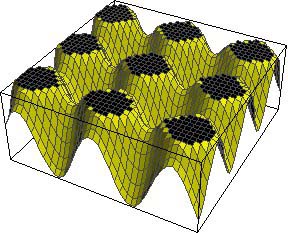
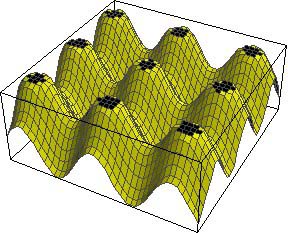
这些斑点的大小依赖于所谓的“阈值”。激活物的浓度可以想象成山丘地貌，只有一定浓度的激活物（即高度）才能激活色素。如果这个阈值很大，则只可以看到山丘顶端很小的顶点，但如果这个阈值降低，则有更多的山丘会被“着色”，斑点会更大，间距也更小。这个机制或许可以解释长颈鹿两个亚种图案的不同：罗斯柴尔德长颈鹿 (Rothschild’s giraffe) 和网纹长颈鹿 (reticulated giraffe)（如本文最前面所示），前者比后者的斑点更小、间距更大。

激活色素的阈值比较低	激活色素的阈值比较高

饱和也是一个重要因素。如果激活物的浓度达到一个最大值（即生成的速率跟分解或者扩散的一样快），则斑点可能会连在一起形成条纹。这种情况被认为发生在斑马身上。

尺寸影响

胚胎在图案形成时的尺寸大小也非常重要。如果抑制物相对于空间尺寸扩散得太快，则只能形成很少的斑点。实际上，激活物浓度的驻波和吉他弦的振动模式非常类似：只有某些合适的波长才能形成。以下示意图展示了在不同尺寸“胚胎”上进行的反应-扩散模拟：长度分别为 $5$, $30$, $150$ 以及 $1000$ 个单位。在小动物上不会产生任何图案，而在非常大的动物上，斑点非常小以至于就像融合在了一起。

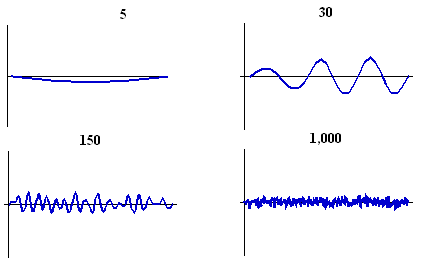不同尺寸的反应—扩散模拟

一些发育生物学家认为这解释了为什么小老鼠或者大象没有任何图案。而在中间，随胚胎尺寸增大有越来越多的图案。如果假定所有的哺乳动物 $d$ （扩散常数）一样，则可以解释为什么仓鼠只有几处斑块而猎豹有成百上千的斑点。

局部区域尺寸也会影响所能形成的图案类型。动物的尾巴可以想象成一个半径持续减小的圆柱体。在根部尺寸足够大，足以形成二维的斑点，但在尾部尺寸则太小。在尾部高浓度的激活物区域环绕着尾巴分布并且连成一体，于是斑点就变成了条纹。因此斑点和条纹的过渡情况可以在猎豹的尾巴上清楚地展现出来。以上数学推论也揭示了为什么有斑点的动物可以有条纹状图案的尾巴，而有条纹图案的动物不会有斑点状图案的尾巴。

图案生成的过程在哺乳动物的胚胎期就已经完成。但有些动物会在长大的过程中更新它们的图案。神仙鱼的图案会随着局部区域的变大而慢慢移动。小鱼身上的条带会在长大过程中分开，新的条纹会出现或者从已有的上面分开以填充任何间隙。

猎豹身上为斑点，尾巴则是条纹状。有条纹状图案的动物不可能有斑点状图案的尾巴。

自然艺术？

触发形成斑点或条纹的扰动一般是成形素生成或扩散过程中速率的统计性偏差。但是胚胎外部的物理性扰动也会有同样的效果。蝴蝶翅膀上的眼斑也被认为依赖上述的原理，虽然涉及到更多的成形素。Marta de Menezes 通过针戳还在蛹中发育的蝴蝶翅膀创作活物艺术。针戳改变了浓度梯度，因而也改变了自然的设计。

扩展阅读

• A. Turing (1952). The Chemical Basis of Morphogenesis. Philosophical Transactions of the Royal Society of London. Available for free download, at participating institutions, from JSTOR.
• J.D. Murray (2001). Mathematical Biology. Published by Springer-Verlag New York Inc.
• D.S. Jones and B.D. Sleeman (2003). Differential Equations and Mathematical Biology. Published by Chapman & Hall.

作者： Lewis Dartnell

翻译 : sci707

2016年11月7日

来源 : https://plus.maths.org/content/how-leopard-got-its-spots